 Department
of
Department
of
Science & Technology Studies
University College London
Nicholas Kollerstrom's
Newton's 1702 Lunar Theory
The Equation of Centre
The astronomers of Restoration England were just beginning
to apply Kepler's first two laws in the preparation of planetary and
solar/lunar tables. The problem was that there was no easy way of finding
the Equation of Centre. 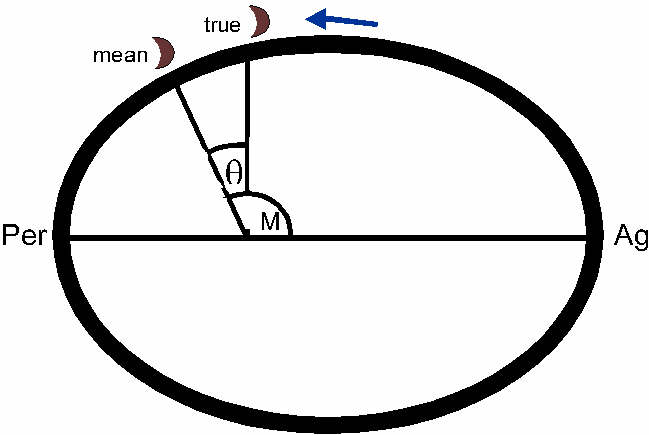 Figure
1 shows the angle called 'mean anomaly' (M), as between the mean moon (moving
with uniform angular velocity around the Earth, at one focus of the ellipse),
and the mean apogee. The 'true' Moon was found by applying an 'equation',
here represented by the angle theta, so its anomaly value is given by {M
- theta}. The Moon is here moving from apogee to perigee, when the true
moon lags behind the mean moon. Equation of Centre tables would give values
for theta, depending on eccentricity and mean anomaly.
Figure
1 shows the angle called 'mean anomaly' (M), as between the mean moon (moving
with uniform angular velocity around the Earth, at one focus of the ellipse),
and the mean apogee. The 'true' Moon was found by applying an 'equation',
here represented by the angle theta, so its anomaly value is given by {M
- theta}. The Moon is here moving from apogee to perigee, when the true
moon lags behind the mean moon. Equation of Centre tables would give values
for theta, depending on eccentricity and mean anomaly.
Other methods of finding the Equation of Centre, which
did not assume an elliptical shape to the orbit, were much simpler
to solve (so-called equant methods) and were still being used. In the 1670s,
Newton was hardly familiar with the idea of using the Kepler second law
in an astronomical context (though Bernard Cohen and Curtis Wilson have
disagreed on this matter). Tables would give the Equation of Centre for
the lunar orbit, as the angle between the mean Moon and its 'equated' ie
more correct position on an elliptical orbit, where its magnitude depended
upon the eccentricity E and the Moon-apse angle known as the 'anomaly'
(A-M, where A and M are the apse line and lunar longitudes).
The first three terms of the modern Equation of Centre
are:
(2E-E3/4)sin(A-M) - 5/4E2sin2(A-M) + 13/12E3sin3(A-M)
...
The first two terms (ie, using only E and E2
values) are generally adequate for the computations performed here.
Flamsteed's 'Equation of Centre'
tables in his 1681 Doctrine of the Sphere agreed with the values
given by this equation, to within six arcseconds, indicating that Kepler's
second law was being applied before the Principia was published
(Thoren, 1974, Gingerich and Welther, 1974). Earlier, the tables published
in 1673 in Horrock's Opera Omnia had only slightly less accurate
Equation of Centre tables, with a maximal error (I found) of 13 arcseconds.
We are not told who prepared these tables, but it may have been Flamsteed. 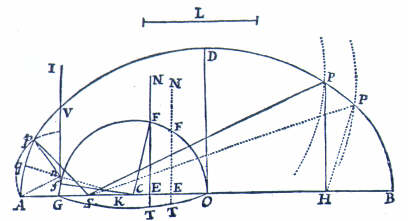 This
early British use of Kepler's second law has received scant recognition.
It is evident that Flamsteed was using a solution of 'Kepler's equation',
to give effectively exact Equation of centre values. He may have been the
first to do this. The reconstruction of TMM (TMM
Replica) used the modern Equation of Centre, as Newton did not specify
any procedure for obtaining it.
This
early British use of Kepler's second law has received scant recognition.
It is evident that Flamsteed was using a solution of 'Kepler's equation',
to give effectively exact Equation of centre values. He may have been the
first to do this. The reconstruction of TMM (TMM
Replica) used the modern Equation of Centre, as Newton did not specify
any procedure for obtaining it.
This diagram from Newton's Principia (Propn 31,
Book 1) show his geometrical approach to finding the equation of centre,
where S is the focus of the ellipse and and AB is its apse line.
The contents of this page remain
the copyrighted, intellectual property of Nicholas Kollerstrom. Details.
rev: February 1998
 This
early British use of Kepler's second law has received scant recognition.
It is evident that Flamsteed was using a solution of 'Kepler's equation',
to give effectively exact Equation of centre values. He may have been the
first to do this. The reconstruction of TMM (TMM
Replica) used the modern Equation of Centre, as Newton did not specify
any procedure for obtaining it.
This
early British use of Kepler's second law has received scant recognition.
It is evident that Flamsteed was using a solution of 'Kepler's equation',
to give effectively exact Equation of centre values. He may have been the
first to do this. The reconstruction of TMM (TMM
Replica) used the modern Equation of Centre, as Newton did not specify
any procedure for obtaining it.
 Department
of
Department
of
 Figure
1 shows the angle called 'mean anomaly' (M), as between the mean moon (moving
with uniform angular velocity around the Earth, at one focus of the ellipse),
and the mean apogee. The 'true' Moon was found by applying an 'equation',
here represented by the angle theta, so its anomaly value is given by {M
- theta}. The Moon is here moving from apogee to perigee, when the true
moon lags behind the mean moon. Equation of Centre tables would give values
for theta, depending on eccentricity and mean anomaly.
Figure
1 shows the angle called 'mean anomaly' (M), as between the mean moon (moving
with uniform angular velocity around the Earth, at one focus of the ellipse),
and the mean apogee. The 'true' Moon was found by applying an 'equation',
here represented by the angle theta, so its anomaly value is given by {M
- theta}. The Moon is here moving from apogee to perigee, when the true
moon lags behind the mean moon. Equation of Centre tables would give values
for theta, depending on eccentricity and mean anomaly.