FLAMSTEED’S LUNAR DATA, 1692-95, SENT TO NEWTON
Journal for History of Astronomy, xxvi (1995), 237-246
NICHOLAS KOLLERSTROM, University College London, and BERNARD D. YALLOP, Royal Greenwich Observatory, Cambridge
Foreword 2004
In the last years of Britain’s Royal Greenwich Observatory, Bernard Yallop, Head of its Nautical Almanac Office, decided to look back and assess the accuracy of Britain’s first Astronomer Royal, using modern programs. His expertise in positional astronomy is rare – indeed, I know of no-one else who could have done this. Nearly all of Flamsteed’s data which was used by Newton to develop the lunar theory was lost, presumably by Newton handing it onto Halley. Here we examine the one and only Table of data that remains, and see how Flamsteed had indeed managed to attain an accuracy of around 20 arcseconds for the Moon and five arcseconds for stars: I don’t know which is more awesome, that he managed to achieve that or that Bernard Yallop managed to show this by his subtle reconstruction, of conditions a few centuries ago. The Table contrasts this observational accuracy with errors in theory of 6-8 arcminutes, from Flamsteed’s use of Horrox’s lunar theory. This was what interested Newton: Tom Whiteside called his 1975 tercentenary essay ‘Newton’s Lunar Theory: From High Hope to Disenchantment’ and we here look at Newton’s period of ‘high hope’ around 1694/5 when he believed that, using this data, he would be able to derive a gravity-based lunar theory. We also looked at some of Edmond Halley’s lunar measurements, Flamsteed’s successor, and found not surprisingly that they were quite an improvement. There is a long tradition of saying that there was something wrong with Halley’s observations, or that they were never published - here refuted. This positional astronomy study (nowadays a vanishing art) was fairly essential for my PhD, completed in 1995 and now published as ‘Newton’s Forgotten Lunar Theory.’ www.greenlion.com/Roar2000text.html Flamsteed has always received ‘blame’ for frustrating Newton’s endeavour to achieve his hoped-for lunar theory and this article endeavours to exorcise that persistent myth.
Introduction
In September 1694, Isaac Newton paid a visit to the newly established observatory at Greenwich, accompanied by David Gregory. John Flamsteed, the first Astronomer Royal, showed them several pages of observed minus calculated lunar positions, indicating errors inherent in the current lunar theory. This appears to have been the stimulus for Newton’s great endeavour with lunar theory (1). Flamsteed agreed to send on his set of fifty comparisons of observed minus predicted positions, together with an additional hundred observations he had made using the Mural Arc (2). The original Mural Arc of the Greenwich Observatory was erected in September 1689. A recent account has described it as being “the finest and most exact astronomical instrument constructed to date” (3).
Newton requested unprocessed lunar data, asking in November 1694 that Flamsteed should “communicate to me the Right Ascensions and apparent meridional altitudes of ye Moon as you have found them in yr observations without allowing for the refraction and parallax I will take care of all the rest … (4). Unfortunately no record remains of the exact data sent, so that we do not know to what extent Flamsteed complied with this request.
In February of the next year Table 1 was sent to Newton (5), containing sixteen lunar limb observations given in right ascension and North Polar Distance (i.e. 90° - declination), their conversion to ecliptic longitude and latitude as required for lunar theory, and a comparison with theoretically predicted positions, using the Horroxian method given in Flamsteed’s Doctrine of the sphere of 1681. Table 1 is all that remains of the lunar data sent by Flamsteed to Newton, apart from some stellar transits. It would seem more to resemble the tables that Gregory and Newton were shown in their visit of September 1694, than the later observations as supplied by Flamsteed.
A Request for Raw Data
Much of the interest surrounding the lunar data has revolved around Newton’s ire that erupted in a letter of 9 June 1695, with the claim that “these and almost all your communications will be useless to me unless you can propose some practicable way or other of supplying me wth Observations ... I want not your calculations but your Observations only” (6).
This signified, as Westfall has observed, the closure of Newton’s main period of endeavour with the lunar theory (7). Flamsteed has since been criticised for neglecting to send Newton the lunar data and for sending reduced, rather than raw observations. At the tercentenary of these events a reassessment is appropriate.
On the back of Newton’s next letter, of 29 June, Flamsteed noted with indignation that he had by then sent a total of 243 lunar meridian transit positions to Newton, not including eclipses and appulses (8). A similar number of lunar transits, observed with the Mural Arc, were recorded between 1689 and June 1695. They will be found in Book II of Flamsteed’s posthumously published Historia coelestis Britannica (9). (Book II of the Historia contained raw astronomical data, with lunar and stellar positions given as apparent zenith distances. Clock times for meridian transit readings were given with the daily errors of the clock, sometimes up to half a minute, as Flamsteed preferred not to reset his clocks too often.)
It seems likely that Flamsteed forwarded all of these observations to Newton. Flamsteed’s notebook for the 1690s, now at Cambridge (10), has essentially the same lunar data therein, as does Halley’s pirate edition of the Historia of 1712 (11). The relevant unpublished manuscripts belonging to Newton contain much by way of calculation using Table 1, but not the original data that Flamsteed sent (12).
Newton’s lunar endeavour over this period was one he himself tended to view as a failure (13), perhaps because the desired predictive accuracy was not attained, or because a link with gravity theory was not accomplished. There is a long tradition of blaming Flamsteed for this perceived failure for the supposedly defective way in which he supplied the data (14). For example, it was the view of D. T. Whiteside that:
Rather than send his pristine lunar sightings to be adjusted for such distortions according to Newton’s own preferred schemes of compensation, Flamsteed proudly persisted, to the latter’s intense annoyance, in passing on to him his tabulated “observations” after these had been carefully corrected by him for parallax and refraction, and also, where relevant, according to his own theory of the Sun’s apparent motion (with its further somewhat shaky parameters of terrestrial eccentricity and solar horizontal parallax).... [W]e can begin to picture the treacheries of the new quicksand in which Newton now began to toil … (15)
Were the data unduly theory-laden, and had the “somewhat shaky” parameters produced a “quicksand” for Newton? No solar theory (“his own theory of the Sun’s apparent motion”) was used in Table 1: solar theory was, as Gingerich has shown, a major factor limiting the accuracy of planetary ephemerides of this period (16), but is not required for lunar data. It was employed in constructing the “Equation of the Naturall days” which Flamsteed was regarded as having restored (17), for converting apparent solar time into mean solar time (i.e. GMT); however, this had not been applied to the time-data in Table 1. Meridian solar transits were used to set the clock, but that is a different matter.
Table 1 lists the errors in predicted longitude, as derived from Flamsteed’s Horroxian method, which ranged up to eight minutes of arc, these being quite small for the period: Gingerich found that Connaissance des temps, the main French almanac of the time, had over the period 1695-1701 errors in lunar longitude frequently above 20’ and sometimes up to 30’ of arc (18). In 1683 Flamsteed had expressed the opinion that a predictive accuracy of at best twelve minutes of arc was obtainable by lunar theory in its present state (19). Gingerich found no particular tendency for errors in this period to vary with lunar phase, as had tended to be the case for earlier almanacs, and likewise errors in the Flamsteed data do not vary with lunar phase. Table 1 gives North Polar Distances (“Dist a Pole” (20)) instead of “apparent meridional altitudes” as Newton requested, which were logged in Book II of Historia as “Dist a Vertice”. The coordinates in the table are geocentric. Flamsteed used his own corrections for parallax and refraction to convert from topocentric to geocentric.
TABLE 1. Sixteen sets of observations sent by Flamsteed to Newton on 7 February 1694, giving: the date in Old Style; “Apparent time” measured from noon, i.e. from the solar meridian transit; lunar right ascension 0°-360°, to nearest sixth of an arc minute; North Polar Distance (“dist a P”), as 90° - declination; celestial longitude measured 0°-30° together with zodiac sign; latitudes marked A or B to distinguish north or south of the ecliptic; and observed minus calculated ecliptic latitude and longitude in minutes and seconds of arc for the sixteen observations. The calculated values were determined from Flamsteed’s Horroxian lunar theory published in 1681.
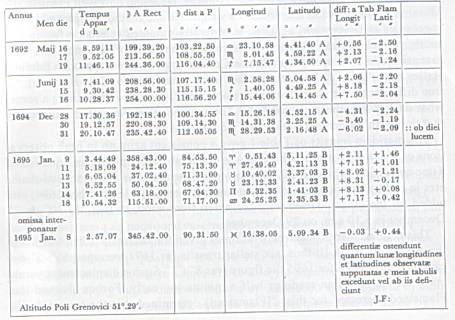
To compute the coordinates from an ephemeris, a conversion from apparent time to mean time is necessary. In a letter accompanying Table 1, Flamsteed said, “I send you included a Copy of my tables of the aequations of Naturall days for four yeares...” (21), but this has not survived. The equation of time (“aequation of the Natural Days”) which Flamsteed applied to obtain Greenwich Mean Time, as it later became called, was published by Flamsteed in 1675 and he produced a more accurate version which Whiston published in 1709 (22).
There was a systematic error in the zenith distance readings, produced by a gradual sinking of the wall on which the Mural Arc was mounted. Flamsteed reckoned that, retrospectively, he could assess this, and in the Historia’s Book II he added an extra column to correct for it.
Modern Investigation of Flamsteed’s Lunar Observations
(a) Equation of Time
We found that Flamsteed’s Equation of Time table of 1709 was usually accurate
to within 10 seconds, with an annual sinusoidal error of 13 seconds (23). His Tompion pendulum clocks lacked temperature correction, and the Historia’s Book II records how these clocks were frequently out by up to ten minutes (24). He preferred not to reset them each day at the solar meridian transit, but instead noted by how much they were fast or slow.
(b) Mural Arc ReadingsFrom the given clock-times of the lunar transits, we found how well Flamsteed’s Mural Arc was oriented due south. He originated the method employed by his successors at Greenwich, of using a vertically mounted telescope facing due south, whereby zenith distances were read as the angle of elevation and right ascensions derived from sidereal time. Concerning this novel approach Edmond Halley remarked in 1711 (in the preface to his pirate edition of the Historia): “... true differences in right ascension are obtained from intervals of time; a somewhat daring hypothesis, it seems” (25). The method used Flamsteed’s discovery that the Earth’s sidereal rotation was isochronous.
The meridian transits of Table 1 gave a consistent azimuth in limb observations of 7’.2 ± 3’ east of south. This was obtained after applying an Equation of Time correction to give GMT, then correcting the readings for lunar semi-diameter in right ascension, subtracted for morning readings (December 1694) and added for the others. Times were measured from noon, so that “17.30” on 28 December is 5.30 a.m. on 29 December.
This displacement concurred with times given for stellar meridian transits in the Historia’s Book II: thus, six stellar transits for 1691 averaged 5’ ± 2’ due east of south, while for 1695 the figure was 8’ ± 2’. Such a displacement would make all his meridian readings half a minute too early. Forbes claimed that Flamsteed corrected for this: “[Flamsteed] determined that the transit on the tropic occurred 38 seconds earlier than it should have done, indicating that the alignment of the instrument was then 92’ west of the true meridian” (26). For a south-facing instrument, a too-early transit implies a deviation to the east! We found no indication that Flamsteed had made such an adjustment.
(c) Comparison with Historia Stellar Positions
Accounts of the construction of Flamsteed’s Mural Arc enabled Allan Chapman (27) to estimate that its accuracy was around twelve seconds of arc. First magnitude stellar apparent zenith distances, given in the Historia’s Book II, generally have an accuracy of around 5” of arc, which more than confirms such an estimate. For example, the meridian transit of the star Pollux as observed on 3 March 1693 had a “Distance a Vertice”, i.e. an apparent zenith distance (AZD) of 22° 44’ 30”. Using Flamsteed’s estimate of the latitude of Greenwich, 51° 28’ 10”, the calculated AZD for Pollux was 22° 44’ 34”.
Reconstruction of stellar positions for a given epoch involves only refraction correction, not parallax or obliquity as is required for lunar readings. Taking one star for each of the dates in Table 1, as recorded in the Historia’s Book II, except for 9 January when no star was recorded, we computed their AZDs (28), comparing them with the values given (using AZD = ZD - refraction, where refraction depends on altitude (alt), and alt = 90°- ZD). This gave a mean error of -4” ± 10”. The accuracy of the lunar AZDs in the Historia’s Book II corresponding to the 16 NPDs of Table 1 was thereby checked. For 9 January the Historia showed no lunar transit recorded; in the fifteen others we found the mean error was -2” ± 42”. Clearly this error was about four times larger than for his stellar AZD values.
(d) Parallax and Refraction CorrectionsThe North Polar Distance readings in Table 1 have been corrected for parallax and refraction. These corrections were investigated by comparing the column for “North Polar Distance” in Table 1 with apparent zenith distances as recorded in the Historia’s Book II for the same transits, where:
North Polar Distance = AZD - latitude + 90°.
In Table 1, Flamsteed used 51° 29’ for latitude.
The parallax correction varies as cosine of altitude with a maximum value of about half a degree. Since refraction and parallax both decrease with increasing altitude in a similar way, we were unable to separate their effects in this small data set.
The errors in NPD of Table I were found to vary with cosine of altitude: for the nine values with lunar altitudes less than 30°, the mean error in altitude was 2’. 1, while for the seven positions with altitude greater than 35°, the mean error was only 0’.5; i.e. the low-altitude lunar sightings were considerably less accurate than the higher ones. These errors would tend to suggest an imperfect parallax theory, except that they are rather too large for that.
Newton sent seasonally adjusted tables of refraction to Flamsteed in November 1694, followed by a further table in March 1695, claiming the latter was accurate to one second of arc above 10° and to two below (29). According to Eric Forbes (30) Flamsteed used these tables. The minimum altitude in the lunar data is 12°, where we estimated the error in Newton’s refraction tables as around thirty seconds of arc, whilst at 30° altitude, the error is around ten seconds31 - an order of magnitude greater than that claimed by Newton, yet inadequate to account for the errors present in Flamsteed’s NPD readings. Errors from parallax and refraction would appear first in the NPD values, whence they would affect mainly the ecliptic latitudes, presumably accounting for their lesser accuracy as compared with the ecliptic longitudes.
If we compare the mean error in the NPD values, given below, with those for the Historia’s corresponding AZD values, a larger standard error is evident. A systematic error of over a minute is present in the NPD data, partly because the value Flamsteed adopted for the latitude of Greenwich was out by half a minute (32). With only sixteen readings, we could not separate the corrections he applied for refraction and parallax, which would have enabled us to find out how the errors in NPD depended upon altitude. Manuscript data sent to us by Frances Willmoth from the RGO Archives (33) contained the actual reduction of the first six observations of Table 1. The calculations indicate that errors of his estimates of refraction, semi-diameter and parallax of the Moon are insufficient to explain the altitude dependence of the errors.
(e) Obliquity of the Ecliptic
For conversion from right ascension and declination into latitude and longitude a value for the obliquity of the ecliptic is required, for which Flamsteed used 23° 29’ 00” (34), as likewise did Cassini (35). The actual value over the period covered by Table 1 was a mere 12” less. For comparison, Streete’s Astronomia Carolina (1710, edited by Halley) gave 23° 28’, while Newton in 1694 recommended the value of 23° 29’ 12” (36).
(f) Lunar Latitude and Longitude
To investigate the accuracy of the observations in Table 1, calculated lunar positions accurate to one or two arc seconds are required. We used The improved lunar ephemeris (ILE), specified by reference number j = 2, which is accurate to better than a second of arc (37).
Table 1 presents four columns of lunar-limb meridian-transit positions. A comparison of ILE calculated values for the sixteen times specified gave the mean errors in seconds of arc for these lunar positions as:
RA -1”±41”; NPD +87”±54”; longitude -15”+48”; latitude +84”±52”.
The mean systematic error of these ecliptic longitudes is merely -15” of arc. Table 1 gives observed transits of the limb, and so lunar semi-diameters have to be applied to the observations before they can be compared with a lunar theory.
TABLE 2. Accuracy of sampled lunar centre observations by Edmond Halley.
| Sampling period | Number | Mean | SD | Coordinates |
| 13 Jan-21 Apr 1722 | 34 | -10” | ±33” | R.A. |
| 21 Jun-02 Aug 1732 | 20 | -14” | ±20” | longitude |
Halley’s Lunar Observations
A comparison with the observations of Edmond Halley, Flamsteed’s successor as Astronomer Royal, that were published posthumously in 1749, is of interest. Halley’s published lunar limb transits were in mean, not apparent time, making him the first astronomer whose data were published using GMT. There is a widespread view that “Halley’s observations scarcely attained the accuracy demanded for their purpose” (38). Francis Baily, as the first President of the Royal Astronomical Society, expressed this opinion (39).
A check on Halley’s azimuth readings showed that, for fifty limb observations at the beginning of 1722, they were 0’.1 ± 0’.8 west of south, which is a much closer alignment than was the case for Flamsteed’s observations.
Halley recorded some 2,200 lunar sightings through one Saros period, 1722-40. For the first five years these were published as limb observations in right ascension, then later he changed to the longitude of lunar centre, the latter being closer to what was required for the testing of a lunar theory as was his goal. We computed lunar limb positions using the same method as for Flamsteed’s observations, converting from geocentric to topocentric coordinates. Estimates of his mean errors are given in Table 2. Halley did not prepare any accompanying NPD or latitude values for publication. The errors shown here are considerably smaller than those of Flamsteed, implying that these lunar transit measurements of Halley were the most accurate up to that date.
They are a significant improvement upon Flamsteed’s and suggest that claims about his incompetence in this respect are totally unfounded. His positional data may have been deemed inaccurate after they were eventually published in 1749, but that is a different matter. Improvements in the longitude arise because Halley used a newly constructed mural quadrant from 1725 onwards, whilst before that he had only a portable quadrant to work with (40).
Conclusions
There is little doubt that the data sent by Flamsteed to Newton comprised the most accurate solar-lunar positional observations then made. His method applied the new technologies of eyepiece micrometry, screw gauge adjustment and Tompion clocks, and initiated the distinctive Greenwich approach of a vertically mounted telescope measuring right ascension by sidereal time.
The loss of these data is curious and regrettable, and prohibits a clear resolution of the centuries-old controversy. It seems questionable whether the observations supplied by Flamsteed to Newton inhibited the mathematician through being laden with undue theoretical assumptions. Taking Curtis Wilson’s estimate that Newton’s lunar theory as published in 1702 was accurate to within seven or eight minutes of arc (41), the data here examined would have been of an entirely adequate accuracy and reliability. Nevertheless, Newton believed that his theory was working to a higher degree of accuracy, as shown by the amplitude of his smallest term of 54 arc seconds. This term was present in both the 1702 and 1713 versions of his lunar theory (42). Flamsteed’s observations were capable of correcting the empirical terms of the theory so that it would be able to predict the position of the Moon to about two minutes of arc in the short term. Such a lunar theory was still short of that required to solve the longitude problem. It is desirable to make a more thorough analysis of the lunar data recorded in the Historia’s Book II (and identically in Halley’s 1712 edition) that were presumably sent to Newton.
We found that Halley’s observations of the Moon, which covered the period of one Saros, and are far more numerous, had smaller random errors than Flamsteed’s, and should therefore have been sufficient to solve this aspect of the longitude problem for a much longer period of time.
We further suggest that it would be worthwhile to re-reduce both the Flamsteed and Halley data using an accurate modern lunar theory, along the lines here indicated, to find their true precision. Amongst other things, it could be used as a lever to improve modern integration ephemerides over long time scales.
References
1. “Memoranda by David Gregory”, The correspondence of Isaac Newton, iv, ed. By H.W. Turnbull (Cambridge 1967; hereafter: Correspondence), 7; Flamsteed’s diary for 1 September 1694, in
F. Baily, An Account of the Revd. John Flamsteed (1835; London, 1966), 61. 2. Correspondence, 8; R. S. Westfall, Never at rest (Cambridge 1980), 541. 3. Allan Chapman, Dividing the circle (Cambridge, 1990), 57.
4. Newton to Flamsteed, 17 November 1694, Correspondence, 46-48, p. 48.
5. Flamsteed to Newton, 7 February 1695, Correspondence, 83-85, p. 85; original in Cambridge University Library Add. 3979, f. 29.
6. Newton to Flamsteed, 29 June 1695, Correspondence, 133-4.
7. Westfall, Never at rest (ref. 2), 546.
8. Memorandum written on back of Newton’s letter of 29 June 1695, Correspondence, 135-6.
9. J. Flamsteed, Historia coelestis Britannica, ii (London, 1725), 152-280.
10. “A copy of the observations made with the Mural Arc, from Sept. 11, 1689 to Dec. 19, 1693”,
Royal Greenwich Observatory Archives, Cambridge University Library, RGO 1/15.
11. J. Flamsteed, [E. Halley (ed.)], Historia coelestis libri duo (London, 1712), II, 51-71.
12. Royal Greenwich Observatory Archives, Cambridge University Library Add. 3966, 13-15.
13. Newton to Flamsteed, 16 January 1699, Correspondence, 296; Westfall, Never at rest (ref. 7), 547; Curtis Wilson, “Predictive astronomy in the century after Kepler”, The general history of astronomy, ii A, ed. by R. Taton and C. Wilson (Cambridge, 1989), 161-206, p. 206; idem, “The Newtonian achievement in astronomy”, ibid., 233-74, p. 267.
14. Baily, op. cit. (ref. 1), 708-9.
15. D. T. Whiteside, “Newton’s lunar theory: From high hope to disenchantment”, Vistas in astronomy, (1976), 317-28, p. 322.
16. O. Gingerich and B. Welther, Planetary, lunar and solar positions, A.D. 1650-1805 (Cambridge, Mass., 1983), p. xv.
17. William Whiston, Astronomical lectures (London, 1715), 335; Derek Howse, Greenwich time and the discovery of longitude (Oxford, 1980), 38.
18. Gingerich and Welther, op. cit. (ref. 16), p. xxi.
19. John Flamsteed, “A letter from Mr Flamsteed”, Philosophical transactions, xii (1683), 404-12, p.405 (quoted in J. Harris’s Lexicon technicum of 1704 under “Moon”).
20. Flamsteed would have generated the North Polar Distance in Table I from:
NPD = zenith distance - parallax + refraction + 90° - latitude.
21. Flamsteed to Newton, op. cit. (ref. 5), 83.
22. William Whiston, “A collection of astronomical tables”, in Astronomical lectures (ref. 17), new pagination, 2-3.
23. D. W. Hughes, B. D. Yallop and C. Y. Hohenkerk, “The equation of time”, Monthly notices of the Royal Astronomical Society, ccxxxviii (1989), 1529-35.
24. The column for uncorrected clock-time readings was called “Tempora per Horologium oscillatorium” in Flamsteed’s Historia, while his clock (or “apparent”) time corrected by solar noon transit was entitled “Tempora vera apparentia”.
25. Halley (ed.), op. cit. (ref. 11), preface.
26. Eric G. Forbes, Greenwich Observatory, i (London, 1975), 48.
27. Chapman, Dividing the circle (ref. 3), 58; Chapman’s earlier estimate was 15 seconds, see Allan Chapman, The Preface to John Flamsteed ‘s Historia Coelestis Britannica (Greenwich, 1982), 5.
28. For reconstructing the historical lunar AZDs (“Dist a Vertice Correcte”) the formula (see below) is:
AZD = zenith distance + parallax - refraction - oblateness,
where oblateness is a correction for the non-spherical shape of the Earth.
29. Newton to Flamsteed, 17 November 1694, Correspondence, 49; 15 March 1695, ibid., 95. The latter table was published in E. Halley, “Some remarks on the allowances to be made for the refraction of the air”, Philosophical transactions, xxxi (1721), 169-172, p. 172.
30. Eric G. Forbes, “A new theory of astronomical refraction”, The Gresham Lectures ofJohn Flamsteed (London, 1975), 65-69, p. 68.
31. Computation kindly performed by Catherine Hohenkerk, at the RGO’s Nautical Almanac Office, using a program based on “The computation of angular atmospheric refraction at large zenith angles”, by C. Y. Hohenkerk and A. T. Sinclair, NAO Technical Note, no. 63 (Herstmonceux, 1985), and inserting the conjectural parameters of 1010 mb pressure and temperatures of-5°C, 10°C, 10°C and 15°C for winter, spring, autumn, and summer, respectively.
32. Flamsteed wrote to Newton in 1695, that his latitude came to 51 ° 29’ 00” “allowing the refractions of ye table you sent me” (9 January 1695, Correspondence, 77-78, p. 78). However on 16 July 1713 he informed Sharp that “in the year 1690, it was determined by the Mural Arc, 51 ° 28’ 30”” (Baily, op. cit. (ref. 1), 302); the modern value for the latitude of his Mural Arc is 51 ° 28’ 38”.
33. Royal Greenwich Observatory Archives, Cambridge University Library, RGO 1/54, ff. 142-5.
34. Given observed values of α and δ (right ascension and declination) and λand β (the ecliptic latitude and longitude) of the Moon, the obliquity ε that Flamsteed used is determined from the equation:
tan ε = (sinλ tanδ - sina tanβ/ (tanβ tanδ + sin a sinλ).
35. Wilson, op. cit. (ref. 13), 191.
36. Newton to Flamsteed, 26 January 1695, Correspondence, 73-76, p. 75.
37. Improved lunar ephemeris (Washington, D.C., 1954). Improvements to ILE (j = 2); “Explanation, Moon”, The astronomical ephemeris (Washington, D.C., and London, 1972), 539, were incorporated in the computer program.
38. W. H. McCrea, Royal Greenwich Observatory: An historical review issued on the occasion of its tercentenary (London, 1975), 10.
39. Francis Baily, “Account of the astronomical observations of Dr Halley”, Memoirs of the Royal Astronomical Society, viii (1835), 169-90, p. 189.
40. Derek Howse, Greenwich Observatory, iii (London, 1975), 21, 113.
41. 41. Wilson, op. cit. (ref. 13), 201.
42. N. Kollerstrom, “The achievement of Newton’s ‘Theory of the Moon’s Motion of 1702”, Ph.D. thesis, University of London, 1995.
Formulae used
NPD = 90° - declination, where NPD is North Polar Distance.
ZD = latitude - declination = 90° - altitude, where ZD is the Zenith Distance of the body.
AZD = ZD + parallax - refraction – oblateness for Moon
AZD = ZD - refraction for stars, where AZD is the Apparent Zenith Distance and parallax = π sin(ZD), and π is the horizontal parallax.
oblateness = -12” sin (altitude) - 2” cos (altitude), for the latitude of Greenwich
lunar radius = 1 / sin π, in Earth radii, semi-diameter of the Moon = 0.2725 it, in the same units as π
NPD = AZD - parallax + refraction + 90° - latitude, Flamsteed’s procedure