Department
of
Science & Technology Studies
University College London
Nicholas Kollerstrom's
Newton's 1702 Lunar Theory
The Paradox of 1713: Shape of the Lunar Orbit
The
first edition of the Principia (1687) contained nothing that was
of practical use to astronomers in regard to lunar theory. Its celebrated
'Moon-test' was a one-body problem, dealing merely with uniform circular
motion around an immobile force-centre. The chief addition to the Second
Edition of the Principia of 1713 was extensive new lunar theory.
A dual-track policy was there pursued, of demonstrating how each of the
lunar 'equations' were derivable from gravity theory, while also trying
to maintain TMM largely intact, e.g. it specified mean motions for Sun,
Moon, nodes etc.
The Principia arguments were formulated in terms
of absolute sidereal space and so used sidereal periods, whereas
TMM was formulated in terms of the tropical reference--i.e., measuring
celestial longitude as astronomers did in practice, from the Vernal Point.
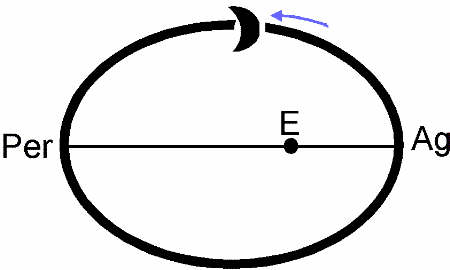
A more serious problem arose from the Horroxian theory's assumption, that
the Moon's motion was elliptical. [figure
1] Using Kepler's first two laws, it viewed
the lunar orbit as an ellipse with Earth at one focus. It thus gave the
lunar orbit an eccentricity of 0.05505. The ellipse revolved once per nine
years in sidereal space (Book III, Propn. 35, Scholium).
That
would have been fine, except that Newton had also developed an 'explanation'
for the inequality know as the Variation, as
discovered by Tycho Brahe and Kepler. This put the Moon in an elliptical
orbit with the Earth at its centre, not at one of the foci.
[figure 2] The short
(minor) axis of this ellipse pointed towards the Sun, so that this ellipse
revolved annually in space. Its eccentricity was three times
larger than the earlier-mentioned ellipse, of the monthly apogee-perigee
orbit. This Variation ellipse allowed Newton to account for why lunar motion
was slightly faster at the Full and New positions than at the quarters,
and his three-body computations credibly explained why solar gravity would
deform a circular orbit in this manner (Book III, Propn. 29).
Each of these models would have been O.K. separately,
but it was far from evident as to how they could be added together. This
mind-wrenching paradox may have been why Newton told Halley that the Moon
was the one subject which made his head ache. A discussion of this paradox
is contained in a forthcoming article by Curtis Wilson, 'Newton on the
Moon's Variation and Apsidal Motion.' Of these two ellipse models Wilson
observed, 'The Variational orbit and the Horrocksian ellipse implied two
disparate pictures of the lunar orbit.' The Variation
was derived from gravity theory in /book III of the Principia several propositions
earlier that the TMM-Scholium, as if Newton had more confidence in the
former.
The contents of this page remain
the copyrighted, intellectual property of Nicholas Kollerstrom. Details.
rev: May 1998
