 Department
of
Department
of Science & Technology Studies
University College London
 Department
of
Department
of
Science & Technology
Studies
University College
London
Nicholas Kollerstrom's
Flamsteed's 1681 Lunar
Theory
This was published in 1681 as the 'Doctrine of the Sphere' as a chapter in his patron Jonas Moore's 'New System of Mathematics'. Flamsteed did not put his name to it, though one assumes most people knew who has written it; and, indeed, it was the only thing he ever published in his lifetime, apart from some brief reports in the Royal Society's journal The Philosophical Transactions. He had then been the 'King's Observator' ie Britain's Astronomer Royal, for five years. The lunar theory is basically just Horrock's theory 'polished' as he put it, and with proper annual equations.
|
To download |
For Flamsteed's |
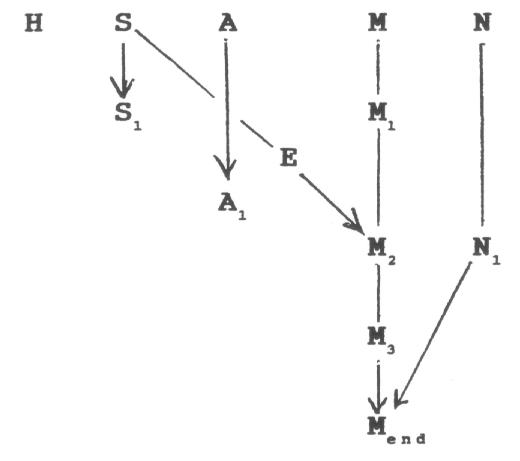
Here are the equivalent formulae for the five mean motions used in Flamsteed's lunar theory, which vary with 't' as the time in days from noon, GMT, of December 31, 1680.
M = 181.7328 + 13.1763946t
S = 290.580 + 0.9856469t
A = 244.1975 + 0.1114083t
H = 96.861 + 0.0000479t
N = 174.2430 - 0.0529550t
Flamsteed in 1681 used two annual equations. For the Sun, in degrees:
where H is aphelion, and S is the mean solar longitude. For the Moon,
where M is mean lunar longitude.
Solar 'anomaly' (the H-S angle) defines a yearly cycle. An equation of centre is required, with two term's have been used for the Sun's Equation, while one will suffice for the Moon as the amplitude of this term is much smaller - 11 arcminutes rather than 2 degrees. [back to flow chart]
The varying eccentricity in the Horroxian model is given by the length TD, where D is the perpendicular dropped from F onto TB. The mean eccentricity is given by the length TC, while its maximum/minimum values are given by TB/TA (T is one focus of the lunar ellipse, where Earth is located, and C is its centre). Flamsteed gives the lunar eccentrity as 0.055237 0.01162, and FCB is the angle A-S1, so we write his eccentricity equation as
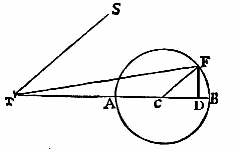
The Horroxian equation for the apse angle is given by the angle FTB, which is more or less obtained from triangle FTD, except that the dimensions given (for maximal apse equation of 11degree 47' 22") don't have quite the same scale triangle:
where (A-A1) is the apse equation and E1 is
the equated eccentricity. It thus becomes zero at each Sun-apse conjunction.
Having obtained the varying eccentricity E, the equated apse and the first equated moon and sun, one is ready for the 'equation' of the lunar ellipse. This involved solving the 'Kepler equation', evidently managed by Flamsteed in the 1670s (see Equation of Centre). The first two terms of the modern equation of centre suffice for this:
In Figure 1, the mean eccentricity of the lunar orbit is given by a length, TC. c is the centre of the ellipse while T is the focus where Earth is located. (In modern terms, the centre-focus distance is expressed as ae where a is radius of the circumscribing circle and e is eccentricity). The varying or equated eccentricity is given by the length TD, with maximal and minimal values reached when the sun meets the apse line. [back to flow chart]
The Variation has a half-lunar period, fortnightly, so that it peaks in the octants (i.e., the 45° positions). While Tycho Brahe who discovered it gave it an amplitude of just over 40', Horrocks diminished it to under 37', which mystified commentators for a while (Jorgensen 1974). [back to flow chart]
This derived from Kepler, having a maximum amplitude 1°30' and zero value per sun-node conjunction--i.e., a six-monthly period. [back to flow chart]
The Reduction converts onto the plane of the ecliptic, from that of the lunar orbit. It appears as modulated by the sun-node angle. [back to flow chart]